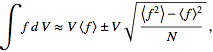Wordtrade.com
Mathematics

Applied Mathemathics

Monte Carlo Methods For Applied Scientists by Ivan T. Dimov (World Scientific Publishing Company) Stochastic optimization refers to the minimization (or maximization) of a function in the presence of randomness in the optimization process. The randomness may be present as either noise in measurements or Monte Carlo randomness in the search procedure, or both. The study of random geometric structures. Stochastic geometry leads to modelling and analysis tools such as Monte Carlo methods.
Common methods of stochastic optimization include direct search methods (such as the Nelder-Mead method), stochastic approximation, stochastic programming, and miscellaneous methods such as simulated annealing and genetic algorithms.  

The Monte Carlo method is inherently parallel and the extensive and rapid development in parallel computers, computational clusters and grids has resulted in renewed and increasing interest in this method. At the same time there has been an expansion in the application areas and the method is now widely used in many important areas of science including nuclear and semiconductor physics, statistical mechanics and heat and mass transfer.

This book attempts to bridge the gap between theory and practice concentrating on modern algorithmic implementation on parallel architecture machines. Although a suitable text for final year postgraduate mathematicians and computational scientists it is principally aimed at the applied scientists: only a small amount of mathematical knowledge is assumed and theorem proving is kept to a minimum, with the main focus being on parallel algorithms development often to applied industrial problems.

A selection of algorithms developed both for serial and parallel machines are provided.

The primary motivation for new developments in Monte Carlo methods is the fact that they are widely used for those problems for which deterministic algorithms hopelessly break down. An important reason for this is that Monte Carlo methods do not require additional regularity of the problem's initial data. The main problem with the deterministic algorithms is that they normally need some additional approximation procedure, requiring additional regularity. Monte Carlo algorithms do not need such procedures. Nevertheless, if one can exploit the existing smoothness of the input data then normally Monte Carlo methods have a better convergence rate than the deterministic methods. At the same time, dealing with Monte Carlo algorithms one has to accept the fact that the result of the computation can be close to the true value only with a certain probability. Such a setting may not be acceptable if one needs a guaranteed accuracy or strictly reliable results. But in most cases it is reasonable to accept an error estimate with a probability smaller than 1. In fact, we shall see that this is a price paid by Monte Carlo methods to increase their convergence rate. The better convergence rate for Monte Carlo algorithms is reached with a given probability, so the advantage of Monte Carlo algorithms is a matter of definition of the probability error.

The second important motivation is that Monte Carlo is efficient in deal­ing with large and very large computational problems: multidimensional in­tegration, very large linear algebra problems, integro-differential equations of high dimensions, boundary-value problems for differential equations in domains with complicated boundaries, simulation of turbulent flows, study­ing of chaotic structures, etc.. At the same time it is important to study applicability and acceleration analysis of Monte Carlo algorithms both the­oretically and experimentally. Obviously the performance analysis of algorithms for people dealing with large-scale problems is a very important issue.

The third motivation for new developments of Monte Carlo methods is that they are very efficient when parallel processors or parallel comput­ers are available. The reason for this is because Monte Carlo algorithms are inherently parallel and have minimum dependency. In addition, they are also naturally vectorizable when powerful vector processors are used. At the same time, the problem of parallelization of the Monte Carlo al­gorithms is not a trivial task because different kinds of parallelization can be used. To find the most efficient parallelization in order to obtain high speed-up of the algorithm is an extremely important practical problem in scientific computing. Another very important issue is the scalability of the algorithms. Scalability is a desirable property of algorithms that indicates their ability to handle growing amounts of computational work on systems with increasing number of processing nodes. With the latest developments of distributed and Grid computing during last ten years there is a seri­ous motivation to prepare scalable large-scale Monte Carlo computational models as Grid applications.

One of most surprising findings is the absence of a systematic guide to Monte Carlo methods for applied scientists. This book differs from other existing Monte Carlo books by focusing on performance analysis of the al­gorithms and demonstrating some existing large scale applications in semi­conductor device modeling. The reader will find description of some basic Monte Carlo algorithms as well as numerical results of implementations. Nevertheless, I found it important to give some known fundamental facts about Monte Carlo methods to help readers who want to know a little bit more about the theory. I also decided to include some exercises specially created for students participating in the course of "Stochastic Methods and Algorithms for Computational Science" at the University of Reading, UK. My experience working with students studying stochastic methods shows that the exercises chosen help in understanding the nature of Monte Carlo methods.

This book is primary addressed to applied scientists and students from Computer Science, Physics, Biology and Environmental Sciences dealing with Monte Carlo methods.

Monte Carlo methods are a powerful tool in many fields of mathematics, physics and engineering. It is known that the algorithms based on this method give statistical estimates for any linear functional of the solution by performing random sampling of a certain random variable (r.v.) whose mathematical expectation is the desired functional.

Definition 1.1. Monte Carlo methods are methods of approximation of the solution to problems of computational mathematics, by using random processes for each such problem, with the parameters of the process equal to the solution of the problem. The method can guarantee that the error of Monte Carlo approximation is smaller than a given value with a certain probability.

So, Monte Carlo methods always produce an approximation of the solution, but one can control the accuracy of this solution in terms of the probability error. The Las Vegas method is a randomized method which also uses

r.v. or random processes, but it always produces the correct result (not an approximation). The computational problem in Monte Carlo algorithms becomes one of calculating repeated realizations of the r.v. and of combining them into an appropriate statistical estimator of the functional J(u) or solution. One can consider Las Vegas algorithms as a class of Monte Carlo algorithms if one allows P = 1 (in this case RN = 0) in Definition 1.2. For most problems of computational mathematics it is reasonable to accept an error estimate with a probability smaller than 1.

The year 1949 is generally regarded as the official birthday of the Monte Carlo method when the paper of Metropolis and Ulam was published, although some authors point to earlier dates.

Ermakov notes that a solution of a problem by the Monte Carlo method is contained in the Old Testament. In 1777 G. Compte de Buffon posed the following problem: suppose we have a floor made of parallel strips of wood, each the same width, and we drop a needle onto the floor. What is the probability that the needle will lie across a line between two strips? The problem in more mathematical terms is: given a needle of length I dropped on a plane ruled with parallel lines t units apart, what is the probability P that the needle will cross a line?; Kalos and Whitlock (1986)]). He found that P = 2//(7t). In 1886 Marquis Pierre-Simon de Laplace showed that the number 71 can be approximated by repeatedly throwing a needle onto a lined sheet of paper and counting the number of intersected lines. The development and intensive applications of the method is connected with the names of J. von Neumann, E. Fermi, G. Kahn and S. M. Ulam, who worked at Los Alamos (USA) for forty years on the Manhattan project 1. A legend says that the method was named in honor of Ulam's uncle, who was a gambler, at the suggestion of Metropolis.

The development of modern computers, and particularly parallel com­puting systems, provided fast and specialized generators of random numbers and gave a new momentum to the development of Monte Carlo algorithms.

Any method which solves a problem by generating suitable random numbers and observing that fraction of the numbers obeying some property or properties. The method is useful for obtaining numerical solutions to problems which are too complicated to solve analytically. It was named by S. Ulam, who in 1949 became the first mathematician to dignify this approach with a name, in honor of a relative having a propensity to gamble. Nicolas Metropolis also made important contributions to the development of such methods.

The most common application of the Monte Carlo method is Monte Carlo integration. In order to integrate a function over a complicated domain , Monte Carlo integration picks random points over some simple domain which is a superset of , checks whether each point is within , and estimates the area of (volume, -dimensional content, etc.) as the area of multiplied by the fraction of points falling within . Monte Carlo integration is implemented in Mathematica as NIntegrate [f, ..., Method->MonteCarlo].

Picking randomly distributed points , , ..., in a multidimensional volume to determine the integral of a function in this volume gives a result

(1)

where

			(2)
			(3)

 

Quasi-Monte Carlo integration is a method of numerical integration that operates in the same way as Monte Carlo integration, but instead uses sequences of quasirandom numbers to compute the integral. Quasirandom numbers are generated algorithmically by computer, and are similar to pseudorandom numbers while having the additional important property of being deterministically chosen based on equidistributed sequences in order to minimize errors.

Monte Carlo methods are connected with computer simulation, and there is a distinction between simulation (where the system investigated and the mathematical model are both stochastic in nature, as in the simulation of a supermarket), and Monte Carlo simulation (where the modeled system is deterministic and the model used is stochastic) as in the case of Monte Carlo integration.

There are many algorithms using this essential idea for solving a wide range of problems. The Monte Carlo algorithms are currently widely used for those problems for which the deterministic algorithms hopelessly break down: high-dimensional integration, integral and integro-differential equa­tions of high dimensions, boundary-value problems for differential equations in domains with complicated boundaries, simulation of turbulent flows, studying of chaotic structures, etc..

An important advantage of Monte Carlo algorithms is that they permit the direct determination of an unknown functional of the solution, in a given number of operations equivalent to the number of operations needed to calculate the solution at only one point of the domain. This is very important for some problems of applied science. Often, one does not need to know the solution on the whole domain in which the problem is defined.

 

The Structural Stabilization of Polymers: Fractal Models by G. V. Kozlov, G. E. Zaikov (New Concepts in Polymer Science: VSP International (Brill) This monograph deals with the structural aspects of transport processes of gases, physical ageing and thermo-oxidative degradation of polymers in detail. Fractal analysis, cluster models of the polymer structure's amorphous state as well as irreversible aggregation models are used as main structural models. It is shown that the polymer structure is often a more important parameter than its chemical construction. Another significant aspect is the structural role in polymer melts oxidation.
The basis for understanding of structural stabilization gives anomalous diffusion of oxidant molecules on the fractal structure for both solid state polymers and polymeric melts. The important part of this problem is structure connectivity characterized by its spectral dimension. Therefore branched (cross-linked) polymers have smaller diffusivity in comparison with linear polymers. Fractal mathematics is used throughout to sharpen measures and tighten explanations. The volume could have used an English-language editor. More

Elementorganic Monomers: Technology, Properties, Applications by L. M. Khananashvili, O. V. Mukbaniani, G. E. Zaikov (New Concepts in Polymer Science: Brill Academic Publishers) The chemical industry in our country and abroad is rapidly developing. It is only natural that the young industry of elementorganic monomers, oligomers and polymers should develop at the same rate. The numerous valuable and sometimes unique properties of these substances account for their wide application in various industries, households, medicine and cutting-edge technologies. That is why contemporary industry produces more than 500 types of silicone monomers, oligomers and polymers, to say nothing of other elementorganic compounds. The synthesis of these elementorganic compounds is based on many different reactions. More

Numerical Modeling of Water Waves, Second Edition, includes CD-ROM by Charles L. Mader (CRC Press) is a well-written, comprehensive treatise of the evolving science of computer modeling of waves. In a very skillful and methodical manner, the Dr. Charles Mader provides new insights on the subject and updates the reader with what is being done with state-of-the-art, high-performance computers which allow for the adaptation of new codes that can result in even more accurate simulations of waves generated from a variety of source mechanisms - whether generated by earthquakes, landslides, explosions, or the impact of asteroids. The book is an outstanding work of scholarship and a valuable reference for any researcher involved or interested in the numerical modeling of waves.

Numerical Modeling of Water Waves discusses the numerical methods for modeling water waves and their applications. This book describes methods developed primarily at the Los Alamos National Laboratory within the last forty years. It explains data on basic fluid dynamics associated with water waves and also addresses advanced techniques for modeling. It provides numerical modeling of the largest historical tsunami wave recorded. Also included is a CD-ROM with FORTRAN codes of numerical methods for water wave modeling, and tsunami wave generation, propagation and flooding. Includes animations of many of the solved problems using these codes.

This second edition of Numerical Modeling of Water Waves de-scribes the technological revolution that has occurred in numerical modeling of water waves during the last decade. A CD-ROM with many of the FORTRAN codes of the numerical methods for solving water wave problems and computer animations of the problems that have been solved using the codes is included with the book. Several PowerPoint presentations describing the modeling results are on the CD-ROM. It will be called the NMWW CD-ROM in the rest of the book.

The objective of this book is to describe the numerical methods for modeling water waves that have been developed primarily at the Los Alamos National Laboratory over the last four decades and to describe some examples of the applications of these methods. Some of the applications of the numerical modeling methods were performed while the author was working at the Joint Institute for Marine and Atmospheric Research at the University of Hawaii, some as Mader Consulting Co. research projects, and the rest as a Fellow of the Los Alamos National Laboratory.

Although the two- and three-dimensional numerical methods for modeling water waves had been available in the 1980's for several decades, they had seldom been used. A major obstacle to their use was the need for access to large and expensive computers. By the 1980's, inexpensive personal computers were adequate for many ap­plications of these numerical methods.

In this book, the basic fluid dynamics associated with water waves are described. The common water wave theories are reviewed in Chapter 1. A computer code called WAVE for personal computers that calculates the wave properties for Airy, third-order Stokes, and Laitone solitary gravity waves is available on the NMWW CD-ROM.

The incompressible fluid dynamics model used for shallow water, long waves is described in Chapter 2. A computer code for personal computers using the shallow water model is called SWAN and is available on the NMWW CD-ROM. The SWAN code is used to model the 1946, 1960 and 1964 earthquake generated Hilo, Hawaii tsunamis, the 1964 Crescent City, California tsunami and the 1994 underwater landslide generated Skagway, Alaska tsunami.

The two-dimensional incompressible Navier-Stokes model used for solving water wave problems is described in Chapter 3. A com­puter code for personal computers using the two-dimensional Navier-Stokes model is called ZUNI and is available on the NMWW CD-ROM. The ZUNI code is used to model tsunami wave propagation and flooding. It is also used to model the effect of underwater barriers on tsunami waves.

The three-dimensional incompressible Navier-Stokes model for solving water wave problems of any type is described in Chapter 4. The equations used in the computer code called SOLA-3D are described and the FORTRAN code is`on the NMWW CD-ROM. The SOLA-3D code is used to model the 1975 Hawaiian tsunami and the 1994 Skagway tsunami by water surface cavities generated by underwater landslides.

It is surprising that most academic and government modelers of water waves have chosen to use shallow water or other incompress­ible models of limited validity for modeling water waves and not use the incompressible Navier-Stokes model since the first edition of this book was published. The severe limitations of the shallow water model are described in Chapter 5.

The generation of water waves by volcanic explosions, conven­tional or nuclear explosions, projectile and asteroid impacts require the use of the compressible Navier-Stokes model. The numerical models and codes for solving such problems have recently become available as part of the Accelerated Strategic Computer Initiative program. A computer code for solving one, two and three dimen­sional compressible problems called SAGE, NOBEL or RAGE is described in Chapter 6 and some of its remarkable capabilities are presented. These include modeling of the KT Chicxulub asteroid impact and the modeling of the largest historical tsunami which oc­curred July 8, 1958, at Lituya Bay, Alaska. The modeling of the Lituya Bay impact landslide generated tsunami and the flooding to 520 meters altitude is described.

A color videotape (VTC–86–4) lecture featuring computer gen­erated films of many of the applications discussed in this book is available from the Los Alamos National Laboratory library. Several web sites have been established that contain additional information and computer movies of the problems described in this book. The major sites are http://www.mccohi.org and httpi/tl4web.lanl.gov/Staff/clm/tsunami.mve/tsunami.html.

Finite Mathematics and Its Applications, Eighth Edition by Larry Joel Goldstein, David I. Schneider, Martha J. Siegel, T. E. Graedel (Prentice Hall) This work is the eighth edition of our text for the traditional finite mathematics course taught to first- and second-year college students, especially those majoring in business and the social and biological sciences. Finite mathematics courses exhibit tremendous diversity with respect to both content and approach. There­fore, in revising this book, we incorporated a wide range of topics from which an instructor may design a curriculum, as well as a high degree of flexibility in the order in which the topics may be presented. For the mathematics of finance, we even allow for flexibility in the approach of the presentation.

This edition maintains a popular student-oriented ap­proach throughout and, in particular, through the use of the following features:

Realistic applications illustrate the uses of finite mathematics in other disciplines. The reader may survey the variety of applications by referring to the Index of Applications located on the front endpapers. Wherever possible, the authors attempt to use applications to motivate the mathematics. For example, the concept of linear programming is introduced via a discussion of production options for a factory with a labor limitation.

They include many more worked examples than is customary in textbooks. Furthermore, they include computational details to enhance comprehension by stu­dents whose basic skills are weak.

More than 2700 exercises comprise about one-quarter of the book, the most im­portant part of the text in our opinion. The exercises at the ends of the sections are usually arranged in the order in which the text proceeds, so that homework assignments may be easily made after only part of a section is discussed. Inter­esting applications and more challenging problems tend to be located near the ends of the exercise sets. Supplementary exercises at the end of each chapter am­plify the other exercise sets and provide cumulative exercises that require skills acquired from earlier chapters. Answers to the odd-numbered exercises from the sections and answers to all the supplementary and chapter test exercises are included at the back of the book.

The practice problems are a popular and useful feature of the book. They are carefully selected exercises located at the end of each section, just before the exercise set. Complete solutions follow the exercise set. The practice problems often focus on points that are potentially confusing or are likely to be overlooked. The authors recommend that the reader seriously attempt to do the practice problems and study their solutions before moving on to the exercises.

Although the use of technology is optional for this text, many of the topics can be enhanced with graphing calculators, electronic spreadsheets, and mathematical software. Whenever relevant, we explicitly show the student how to use graphing calculators and electronic spreadsheets effectively to assist in understanding the fundamental concepts of the course. In addition, the text contains appendices on the fundamentals of using graphing calculators and electronic spreadsheets. The powerful mathematical software "Explorations in Finite Mathematics" is packaged with each Student Solutions Manual. Many sections of the book contain specially designed technology exercises intended to be solved with one of these technologies.

In our discussions of graphing calculators, we specifically refer to the TI-83 since this is the most popular graphing calculator. Therefore, most stu­dents will have a book customized to their calculator. Students with other graph­ing calculators can consult their guidebooks to learn how to make adjustments. Had the calculator material been written generically, every student would have to make adjustments. For the same reasons, the discussions of electronic spread­sheets refer to Microsoft Excel.

We have included questions similar to those found on CPA, GMAT, and GRE Economics exams to illustrate further the relevance of the material in the course. These multiple-choice questions are identified with the notation PE (which stands for "professional exams").

Near the end of each chapter is a set of questions that help the student recall the key ideas of the chapter and focus on the relevance of these concepts.

Each chapter contains a detailed summary of the important definitions and re­sults from the chapter serving as a handy study tool for the student. Each chapter has a sample test that can be used by the student to help determine if he or she has mastered the important concepts of the chapter. The answers to the chapter test are given at the back of the book.

Most chapters have extended projects that can be used as in-class or out-of­class group projects, or special assignments. These projects develop interesting applications or enhance key concepts of the chapters.

Among the changes in this edition, the following are the most significant:

• Personal financial decisions section. A section has been added to the end of Chapter 10 that considers financial decisions that students often have to make shortly after graduating from college. The section discusses IRAs, consumer loans, and mortgages. The differences between traditional and Roth IRAs are discussed along with the advantages of starting them early. The common add-on method for computing the finance charges for a consumer loan is presented and analyzed. The section shows how to compare mort­gages having different up-front fees by calculating their APRs, which must be provided by the lender, and their effective mortgage rates, which are used by mortgage analysts to compare mortgages.

• Electronic spreadsheets. An appendix titled "Spreadsheet Fundamentals" has been added. In addition, relevant material on the use of spreadsheets is presented alongside appropriate topics in the book.

• A new chapter project for the Mathematics of Finance chapter provides useful insights into the effects of interest.

• The discussion of sensitivity analysis of linear programming problems has been expanded.

• Additional exercises and updated data. We have added many new exercises (including about two-dozen similar to those appearing in professional exams, such as the GMAT) and have updated the real-world data appearing in exercises and examples.

• Because of great variation in student preparation, we keep formal prerequisites to a minimum. We assume only one year of high school algebra. Furthermore, we review, as needed, those topics that are typically weak spots for students.

This edition has more material than can be covered in most one-semester courses. Therefore, the instructor can structure the course to the students' needs and in­terests. The book divides naturally into four parts. The first part consists of linear mathematics: linear equations, matrices, and linear programming (Chap­ters 1-4); the second part is devoted to probability and statistics (Chapters 5-7); the third part covers topics utilizing the ideas of the other parts (Chapters 8-10); and the fourth part explores key topics from discrete mathematics that are some­times included in the modern finite mathematics curriculum (Chapters 11-13). We prefer to begin with linear mathematics since it makes for a smooth transi­tion from high school mathematics and leads quickly to interesting applications, especially linear programming. Our preference notwithstanding, the instructor may begin this book with Chapter 5 ("Sets and Counting") and then do either the linear mathematics or the probability and statistics.

Mathematics for Chemistry & Physics by George Turrell (Academic Press) This book has been written in an attempt to provide students with the math­ematical basis of chemistry and physics. Many of the subjects chosen are those that I wish that I had known when I was a student. It was just at that time that the no‑mans‑land between these two domains ‑ chemistry and physics ‑ was established by the "Harvard School", certainly attributable to E. Bright Wilson, Jr., J. H. van Vleck and the others of that epoch…

That chemistry and physics are brought together by mathematics is the "raison d'être" of the present volume. The first three chapters are essentially a review of elementary calculus. After that there are three chapters devoted to differential equations and vector analysis. The remainder of the book is at a somewhat higher level. It is a presentation of group theory and some applications, approximation methods in quantum chemistry, integral transforms and numerical methods.

This is not a fundamental mathematics book, nor is it intended to serve a textbook for a specific course, but rather as a reference for students in chemistry and physics at all university levels. Although it is not computer based, I have made many references to current applications ‑ in particular to try to convince students that they should know more about what goes on behind the screen when they do one of their computer experiments. As an example, most students in the sciences now use a program for the fast Fourier transform. How many of them have any knowledge of the basic mathematics involved?

The lecture notes that I have written over many years in several countries have provided a basis for this book. More recently, I have distributed an early version to students at the third and fourth years at the University of Lille. It has been well received and found to be very useful. I hope that in its present form the book will be equally of value to students throughout their university studies.

An Introduction to Stochastic Processes with Applications to Biology by Linda J. S. Allen (Prentice Hall) My goal in writing this book is to provide an introduction to the basic the­ory of stochastic processes and to some of the many biological applications of stochastic processes. The mathematical and biological background re­quired is kept to a minimum so that the topics are accessible to students and scientists in biology, mathematics, and engineering. Many of the biological applications are from the areas of population dynamics and epidemiology due to personal preference and expertise and because these applications can be readily understood.

Interdisciplinary areas such as mathematical biology, biostatistics, and bioengineering are growing rapidly. Modeling and analysis of biological phenomena require techniques and tools from various disciplines. Many recent books have addressed the need for a better understanding of the underlying theory of modeling in biology. However, much more attention has been paid to the area of deterministic modeling in biology than to stochastic modeling, and this book helps to fill the gap.

The topics in this book are covered in a one-semester graduate course offered by the Department of Mathematics and Statistics at Texas Tech University. This book is intended for an introductory course in stochastic processes. The targeted audiences for this book are advanced undergrad­uate students and beginning graduate students in mathematics, statistics, biology, or engineering. The level of material in this book requires only a ba­sic background in probability theory, linear algebra, and analysis. Measure theory is not required. Exercises at the end of each chapter help reinforce concepts discussed in each chapter. To better visualize and understand the dynamics of various stochastic processes, students are encouraged to use the MATLAB programs provided in the Appendices. These programs can be modified for other types of processes or adapted to other programming languages. In addition, research on current stochastic biological models in the literature can be assigned as individual or group research projects.

The book is organized according to the following three types of stochas­tic processes: discrete time Markov chains, continuous time Markov chains and continuous time and state Markov processes. Because many biolog­ical phenomena can be modeled by one or more of these three modeling approaches, there may be different stochastic models for the same biological phenomena, e.g.. logistic growth and epidemics. Biological applications are presented in each chapter. Some chapters and sections are devoted en­tirely to the discussion of biological applications and their analysis (e.g.., Chapter 7).

In Chapter 1, topics from probability theory are briefly reviewed which are particularly relevant to stochastic processes. In Chapters 2 and 3, the theory and biological applications of discrete time Markov chains are discussed, including the classical gambler's ruin problem, birth and death processes and epidemic processes. In Chapter 4, the topic of branching pro­cess is discussed, a discrete time Markov chain important to applications in biology and medicine. An application to an age-structured population is discussed in Chapter 4. Chapters 5, 6, and 7 present the theory and biologi­cal applications of continuous time Markov chains. Chapter 6 concentrates on birth and death processes and in Chapter 7 there are applications to epidemic, competition, predation and population genetics processes. The last chapter, Chapter 8, is a brief introduction to continuous time and con­tinuous state, Markov processes; that is, diffusion processes and stochastic differential equations. Chapter 8 is a non-measure theoretic introduction to stochastic differential equations. These eight chapters can be covered in a one-semester course. One may be selective about the particular applica­tions covered, particularly in Chapters 3, 7, and 8. In addition, Section 1.6 on the simple birth process and Section 2.10 on the random walk in two and three dimensions are optional.

Numerous applications of stochastic processes important in areas out­side of biology, including finance, economics, physics, chemistry, and en­gineering, can be found in the references. This book stresses biological applications and therefore, some topics in stochastic processes important to these other areas are omitted or discussed very briefly. For example, martingales are not discussed and queueing theory is only briefly discussed in Chapter 6.

Throughout this book, the emphasis is placed on Markov processes due to their rich structure and the numerous biological models satisfying the Markov property. However, there are also many biological applications where the Markov restriction does not apply. A stochastic process is dis­cussed in Section 7.2, which is a non-Markovian, age-dependent process be­longing to a class of stochastic processes known as regenerative processes. It is important to note that in some applications the Markov restriction is not necessary, e.g.., first passage time in Chapter 2 and the waiting time distribution in Chapter 5. This latter theory can be discussed in the more general context of renewal theory.

Headline 3

insert content here

WT Main | About WT | Review Links | Contact | Review Sources | Search